改良型DLTS法
深い準位からのキャリア放出に伴う接合容量変化を測定するのが、DLTS法の要点であるわけですが、実のところこの容量変化は、サブfF~pFオーダーのたいへん小さなものです。
測定技術の観点からは、このような微小信号をS/N比よく測定する方法が必要となります。 Langの方法(ボックス・カー方式)は、実のところ微小信号の測定に関しても有効な方法といえます。
実際の測定にあたっては、トランジエント測定は、一つの温度下で繰り返して行われ、信号の平均化によりS/Nを改善することが行われています。
その後、今日に至るまでDLTS法においては、微小信号から、高感度のデータを効率的に得るかという点を目指した改良がおこなわれてきました。
LangのDLTS法は、いわゆるアナログシステムでした。
今日のような高性能なコンピュータのない時代に、高速の信号から情報を抽出する実に巧妙な方法であったといえますが、決して効率的とはいえませんでした。
それは、トランジエント信号のごく一部の情報しか利用していないためということもできるでしょう。
今日では、高性能なパーソナルコンピュータが手軽に使えるため、事態は大きく異なり、DLTSにおける通常μs~sの範囲のトランジエント信号を完全にデジタルデータとして収録することは、比較的容易な技術であるといえます
デジタルデータシステムにおいては、例えば、一つのトランジエントデータを使って、異なる t1 および t2 の組み合わせ測定から時定数の温度変化を求めるという操作は、コンピュータ上でソフト的に行うことができますので、繰り返し降温/昇温を必要とする煩雑な測定は不要となるわけです。
一方、DLTSスペクトルにおけるピーク形状は基本的にブロードなものであるため、準位エネルギーの分解能という観点からは、決して良いものではありませんでした。
近年、デジタル信号処理技術の発展により、DLTS法においては、高感度だけでなく高分解能を目指した工夫が行われています。
PhysTech社のDLTS装置における信号処理では、フーリエ変換法、相関関数法、ラプラス変換法、マルチ指数関数フィッティングおよびICTSスペクトルおよびDLTSスペクトルのデコンボリューションなど種々の手法を用いた解析が可能となっています。
特にHERA-DLTSにおけるラプラス変換を用いた手法は、従来のDLTS法において十分でなかったエネルギー分解能を重視した解析結果を提供できるものであり、DLTS法に新たな可能性を付加したものです。
フーリエ変換式DLTS
DLTSにおける信号処理にフーリエ変換を使う方法は、早くも1982年に報告4)があり、特にDLTFS (Deep Level Transient Fourier Spectroscopy)と呼ばれることがあります。
DLTFS法では、トランジエントデータから、その温度における放出過程の時定数などを直接導出することができます。 ここでいう「直接」とは、一般的なDLTS法におけるスペクトル(温度依存性カーブ)のピークから求める方法のように「間接」的ではないという意味です。
現在のPhysTech社のDLTS装置に使われているこの方法5)の要点は、以下のようなものです。
- 容量トランジエントにおけるN個の測定データを離散フーリエ変換し、その係数:CnD を求めます。
- 対象とする深い準位からのキャリア放出機構を仮定します。 たとえば、一般的な点欠陥における離散準位の場合であれば、以下の式(A-16)のような指数関数的速度過程です。この式をフーリエ級数展開し、その係数:Cn を計算します。
- CnD が、2. で仮定した機構に基づくことを前提として、CnD と Cn の比較から、後者の式に含まれているパラメータが決定され、深い準位のパラメータ(活性化エネルギー、捕獲断面積)や準位濃度が求められます。
指数関数的時間則は、次式で表されます。
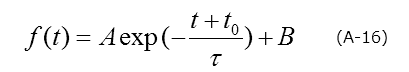
A:振幅、B:オフセット、τ:時定数、to:サンプリングの待ち時間
また、そのフーリエ係数は以下のように表されます。ここで、a、bは、それぞれフーリエ級数展開におけるcos(コサイン)、sin (サイン)の係数、またnはその次数を表しています。

式(A-17),(A-18)の2段目の表式は、τ / Tw による規格化を行ったものであり、t0 / Tw =const. であることから、これらのフーリエ係数が、t0 / Tw だけで表現できることがわかります。
また、以下のような関係が成り立ち、これを用いてトランジエントが指数関数的か否かを評価することができます。
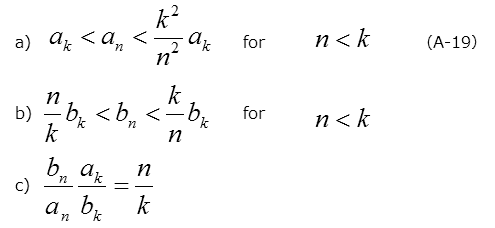
特に、1次と2次の係数を使った場合、以下の関係が得られ、FT1030ソフトウエアの中では、「指数関数クラス」を評価する指標として使われています。
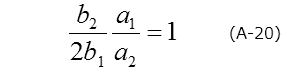
トランジエント波形における振幅は深い準位の濃度に対応するものですが、それぞれのフーリエ係数から計算できます。たとえば、bnの場合ですと、次式で表されます。
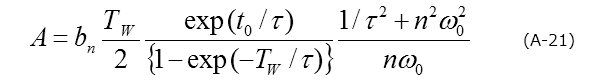
さて、時定数は、2つのフーリエ係数の比から求められます。またそれには、3つの方法があります。

ここで、時定数がトランジエントの振幅や、オフセットと関係なく係数の比だけでも求まるというのは、かなりの利点といえます。
相関関数法(または、重み関数法)6-8)
この方法では次式のように、容量トランジエント波形に対して、ある関数(相関関数またはコリレータ)を掛けたものを、測定時間範囲で積分し、さらにその時間で規格化するという操作をします。
また、コリレータとしては、主として積分範囲で時間積分をすると0(ゼロ)になるようなものが選ばれます。
ここで得られるものは、以下で説明しますように、Langの方法における容量トランジエントにおける差に対応するものと考えることができます。
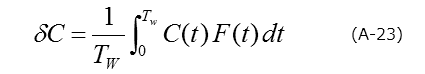
さて、Langの方法を思い出してください。容量トランジエントにおける二つの時間 t1 および t2 における容量値 C(t1)およびC(t2)を測定し、その差 S(T)=△C= C(t1)-C(t2)を求めるものでした。
ここで、F(t1)=1、F(t2)=-1というデルタ関数を考え、次のようなコリレータ:F(t)を考えます。
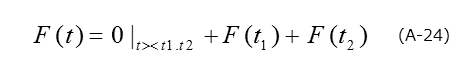
これを使って、式(A-23)の計算をしますと、その結果として、δC = C(t1)-C(t2)が得られることがわかります。
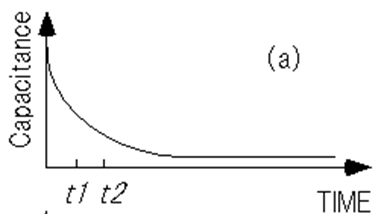
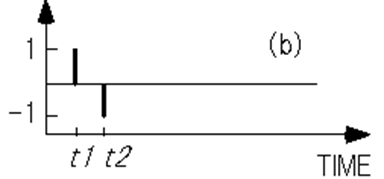
つまり、Langの方法は、式(A-24)のようなデルタ関数をコリレータとした相関関数法と考えることができます(図A-5)。
図A-5. Langによるトランジエント測定
(a) 容量トランジエント波形、(b) デルタ関数(ボックス・カー相関関数)
しかしながら、ボックス・カーコリレータはS/N比という観点からは、あまり良いコリレータではありませんでした。
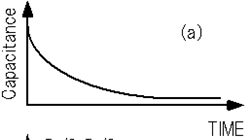
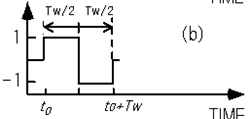
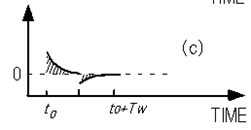
よりS/N比の向上が可能なコリレータとしては、図A-6(b)のような方形波関数8)があります。 このコリレータを図A-6(a)のような容量トランジエント波形に対して使った場合、式(A-23)の計算結果は、図A-6 (c)に示したような0をはさんだ斜線部の面積の差で表されることがわかります。
また、別の見方をすれば、方形波関数は時間t0+Tw/2をはさんで1→-1に極性が反転していますので、上記の面積の差は、Tw/2の区間でのデルタ関数型コリレータでの計算結果を平均したものということもできるでしょう。
図A-6. 方形波関数による相関関数法の説明
(a) 容量トランジエント波形、(b) 方形波コリレータ、(c) 式(A-23)の計算結果の概念図
式(A-23)におけるδCを温度の関数としてプロットしたものが相関関数法におけるDLTSスペクトルです。
スペクトル上に現れたピーク位置の温度が、そのコリレータの種類、TW、t0によって決定される時定数Τmaxを示現する温度ということになります。その関係式は、次式(A-25)で表されます。
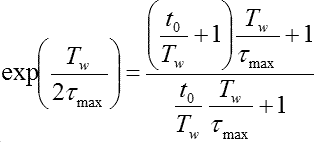
最大条件は直接Τmaxを与える形とはなっていませんが、測定条件としてのTW、t0の値を与えれば、数値計算によってΤmaxを求めることができます。
さて、フーリエ変換の考え方から、上記のフーリエ係数a、bを求める計算は、実は、cos, sin関数をコリレータとした相関関数法と等価ということになります。
特に、これらの1次の係数であるa1およびb1は、FT1030ソフトウエアの中で、それぞれ”Periodwidthscan”法および”Tempscan”法における標準的なスペクトル(縦軸の変数)として使われます。
FT1030ソフトウエアの中では、その他の高次のフーリエ係数や方形波関数を含めた23個のコリレータが用意されています。
これらのコリレータによるDLTSスペクトルの解析によって、多数のアレニウスプロット点が、一度の温度掃引測定から得られるわけです。
また、種々のコリレータは、その感度と分解能に関して、それぞれ異なった特性を有し、一般的にはその間にトレードオフの関係を持ちます9)。
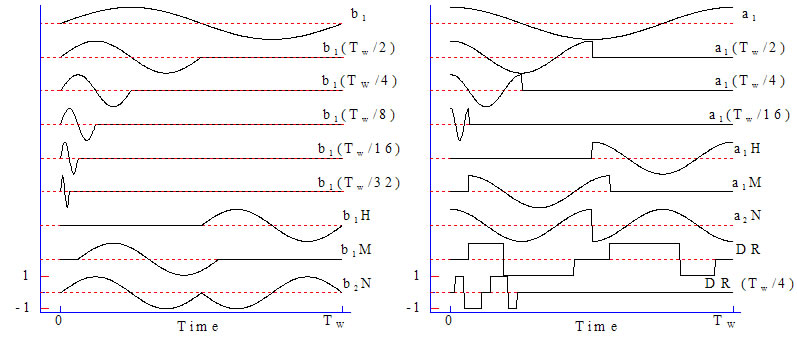
つまり、高感度なコリレータは、エネルギー分解能において劣る傾向があり、またその逆の傾向も成り立ちます。図A-7は、代表的なコリレータを図示したものです10)。
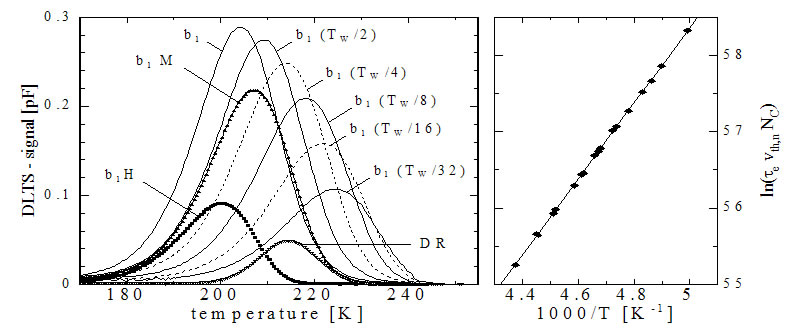
また、図A-8には、これらのコリレータによるDLTSスペクトルと、それぞれのスペクトルにおけるピーク位置から得られたデータによるアレニウスプロットを示しました。
図A-7. コリレータ(相関関数)の例
図A-8. (右)各種コリレータによるDLTSスペクトルの比較
(左) それぞれのピーク位置から得られたデータによるアレニウスプロット
ラプラス変換式DLTS(LDLTS)法11,12)
これまで述べてきました従来DLTS法の欠点は、エネルギー分解能において劣ることでした。
低温で測定したフォトルミネッセンススペクトルは、シャープな励起子発光線よりなる微細構造を持っているため、関連するエネルギー準位に関する情報が高い分解能で得られます。
これに対して、DLTSスペクトルでは概して、微細構造を伴わないブロードなピークしか得られません。
仮に近接したエネルギーを持つ複数の準位が存在したとしても、それらを分離・検出することは困難です。
ラプラス変換式DLTS(LDLTS)法は、このエネルギー分解能に重点を置いた解析方法です。
LDLTS法では、ICTS法と同様な一定温度の下でのトランジエント測定がベースとなります。
非指数関数性を考慮して、トランジエントは、式(A-26)のように放出速度(=時定数の逆数)の連続関数として表されます。
つまりスペクトル密度関数(放出速度の分布):F(s)は、容量トランジエントのラプラス変換ということになります。
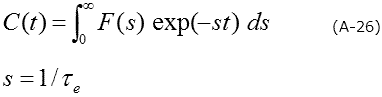
容量トランジエントから、放出速度の分布関数:F(s)を求めるのは、逆ラプラス変換ということになりますが、これはいわゆる数学における「不良設定の逆問題」であり、実験的に求めた容量トランジエントデータから、直ちに一義的な解を得ることは不可能なのです。
これに対してFT1030では、「不良設定の逆問題」に対する一般的な解法であるTikhonov(ティホノフ)の正則化法アルゴリズムをベースとしたソフトウエア:CONTIN(S. Provencher)13)が用いられています。
ここでも正しい解を得るためにはいくつかの条件が必要となりますが、結論として、特にトランジエントデータにおける良好なS/N比が重要であることがわかっています。
仮に近接する二つの準位の時定数比:Τ1/Τ2~2を達成するためには、S/N=1000程度が必要と見積もられています。
ただ、この条件は実験的に可能な範囲と考えられますし、従来のボックス・カー方式、方形波関数方式のDLTSでは、Τ1/Τ2は、それぞれ~12、~15程度が限度であることを考慮しますと、LDLTS法は、近接準位の分離には非常に有効な手段であるといえます。
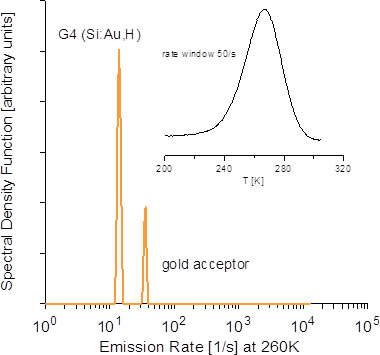
図A-9. 水素を含むSi中Auに関係する準位のLDLTSスペクトル(@ 260K)。挿入図は、従来DLTS法によるスペクトル(レートウインドウ:50 s-1)LDLTSスペクトルでは、近接したエネルギーを持つ二つの準位の存在が示されています。
試料は、Au(金)を拡散させたSiにさらにH(水素)を導入したものです。
右上の挿入図は従来のDLTS法によるスペクトル(レートウンドウ=50 s-1)であり、260K付近に典型的なブロードなピークを持ちます。
このピークは、従来より、Si中のAuによるアクセプタ準位として知られているものです。
これに対して、260Kで測定したLDLTSスペクトル(横軸:放出速度)では、δ関数的なするどい2本のピークが観測されています。
これらのピークに関しては、低速度側がAu-H複合体によるG4と呼ばれる準位(Ea=542meV)、また高速度側がAuアクセプタそのものの準位(558meV)からの放出過程に起因するものであることが報告されています。
従来DLTS法では、1本のピーク(=一つの準位)としてしか認識できなかったわけですが、LDLTS法においては、このような近接した準位の分離が可能であることが示されました。
このように、LDLTS法はこれまでのDLTS法では達成できなかった高エネルギー分解能が大きな特長ですが、その解析の特性上、スペクトルの縦軸強度はトラップ濃度を反映するものではないことに注意が必要です。
したがってトラップ濃度に関しては、例えば従来DLTSと同様な手法での解析が必要です。
さらに、そもそもDLTSピークがブロードニングする原因はいくつか考えられ、決して近接準位の存在だけとは限りません。
例えば、欠陥周りの局所電界による放出速度への影響(Poole-Frenkel効果)などが典型的な例といえるでしょう。
従って、スペクトルを分離することが、常に正しい結果を与えるとは限らないことを忘れてはなりません。
● 参考文献
4) K. Ikeda and H. Takaoka, Jpn. J. Appl. Phys. 21, 462 (1982).
5) S. Weiss and R. Kassing, Solid-State Electronics, 31, 1733 (1988).
6) G. L. Miller, L. V. Ramirez, and D. A. Robinson, J. Appl. Phys. 46, 2638 (1975).
7) L. C. Kimerling, IEEE Trans. Nucl. Sci. NS-23, 1497 (1976).
8) Y. Tokuda, N. Shimizu, and A. Usami, Jpn. J. Appl. Phys. 18, 309 (1979).
9) A. A. Istratov, J. Appl. Phys. 82, 2965 (1997).
10) E. Fretwurst, Workshop on Defects, Hamburg, August 23-2006.
11) L. Dobaczewski, P. Kaczor, L. D. Hswkins, and A. R. Peaker, J. Appl. Phys. 76, 194 (1994).
12) L. Dobaczewski, A. R. Peaker, and B. Nielsen, J. Appl. Phys. 96, 4689 (2004).
13) S. W. provencher, Comput. Phys. Commun. 27, 213 (1982).
14) P. Deixler et al., Appl. Phys. Lett., 73, 3126 (1998).
