トラップパラメータ(準位エネルギーと捕獲断面積)の評価
半導体中の深い準位とバンドとの間のキャリアのやり取りに関しては、SHR(Shockley-Read-Hall)統計2,3) によって記述されます。
準位とバンド間における素過程に関する詳細平衡則から、電子トラップ準位から伝導帯への電子の熱的放出速度: eΤ (前述のτeの逆数)は、次式で表されます。
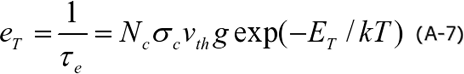
NC:伝導帯の実効状態密度、 σ C:捕獲断面積、 νth:熱速度、 g:準位の縮退度
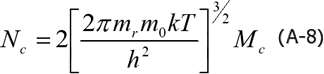
MC :形状因子、 mr:電子の有効質量、 m0:電子の静止質量、 h:プランクの定数
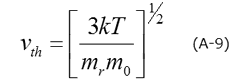
式(A-7)~(A-9)より
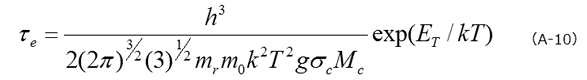
両辺の対数をとることにより、活性化エネルギーを求めるためのアレニウスプロットの基本式(A-11)が得られます。
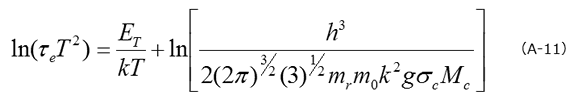
種々の温度における τe を測定し、その温度依存性を考慮して Τ2 を乗じた τeΤ2 を 1/Τ に対して片対数プロット(アレニウスプロット)することで、その直線の傾きから準位のエネルギー:ΕT 、切片から捕獲断面積が求まることになります。
(なお、厳密にはここで求めた捕獲断面積は、有効捕獲断面積: σn,eff = gσc であり準位の縮退度因子を含んだものとなります。捕獲断面積を独立に求める方法としては、「パルスフィリング法」があります。)
前項のDLTSスペクトル測定(図A-4)では、ある深い準位について、その熱的放出時定数が、ある値( τe )になる温度が求まりました。
DLTS法ではこのような測定を、異なる t1 および t2 の組み合わせにより行うことで、別の τe に対応する温度:(Tmax)が得られます。
したがって、例えばこのような測定を5回繰り返すことで、アレニウスプロットには5点のデータ点がプロットできることになります。
● 参考文献
2) W. Shockley and W.T. Read, Phys. Rev. 87, 835 (1952).
3) R. N. Hall, Phys. Rev. 87, 387 (1952).
